Full Factorial DOE with SigmaXL

What is a Full Factorial DOE?

In a full factorial experiment, all of the possible combinations of factors and levels are created and tested. For example, for two-level design (i.e.each factor has two levels) with k factors, there are 2k possible scenarios or treatments.

1. Two factors, each with two levels, we have 2² = 4 treatments
2. Three factors, each with two levels, we have 2³ = 8 treatments
3. k factors, each with two levels, we have 2^k treatments

2^k Full Factorial DOE

Full factorial DOE is used to discover the cause-and-effect relationship between the response and both individual factors and the interaction of factors. Generate an equation to describe the relationship between Y and the important Xs:

Where:

[unordered_list style=”star”]

• Y is the response and X₁, X₂ . . . X_k are the factors
• α₀ is the intercept and α₁, α₂ . . . α_p are the coefficients of the factors and interactions
• ε is the error of the model

[/unordered_list]

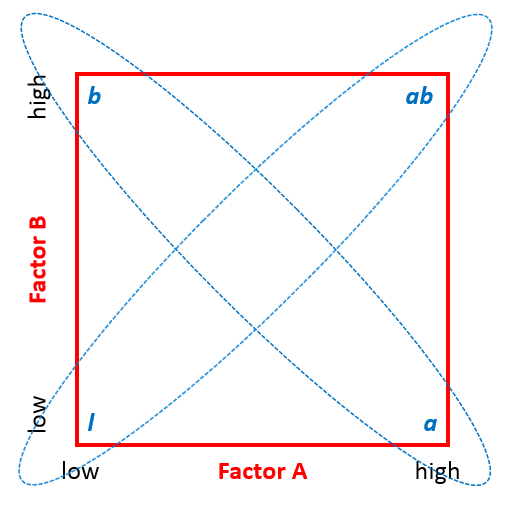
Two-Level Two-Factor Full Factorial

Below is a design pattern of a two-level two-factor full factorial experiment.

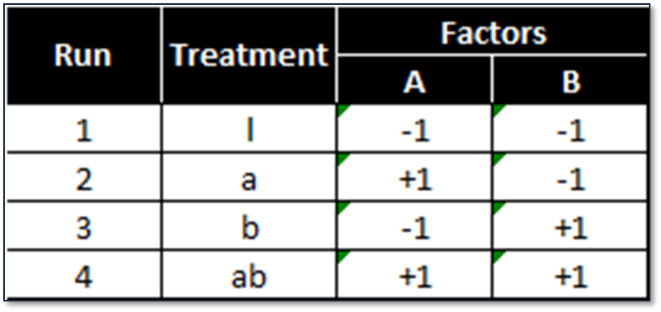
2 (level) raised to 2 (factors) = 4 treatment combinations.

Two-Level Three-Factor Full Factorial

Below is a design pattern of a two-level three-factor full factorial experiment.

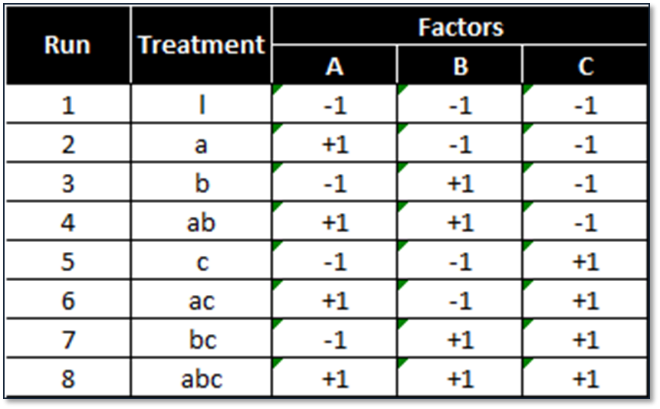
2 (levels) raised to 3 (factors) = 8 treatment combinations.

Two-Level Four-Factor Full Factorial

Below is a design pattern of a two-level four-factor full factorial experiment

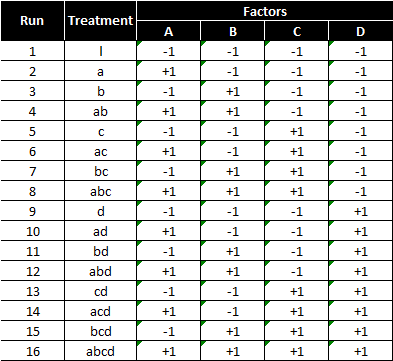
2 (levels) raised to 4 (factors) = 16 treatment combinations

Two-Level Five-Factor Full Factorial

Below is a design pattern of a two-level five-factor full factorial experiment

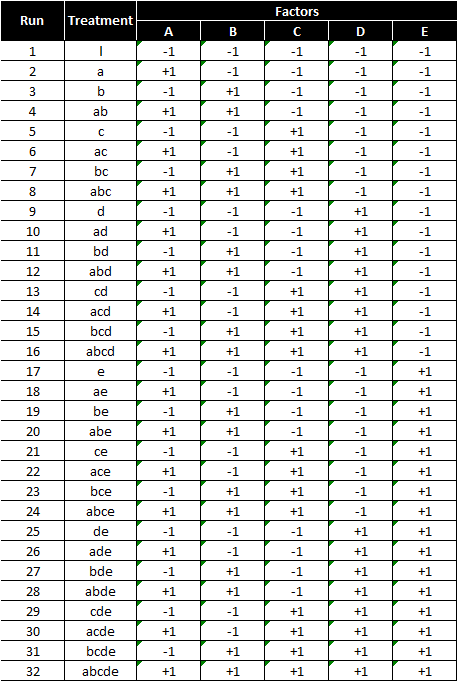
2 (levels) raised to 5 (factors) = 32 treatment combinations

Order to Run Experiments

The four design patterns shown earlier are listed in the standard order. Standard order is used to design the combinations/treatments before experiments start. When actually running the experiments, randomizing the standard order is recommended to minimize the noise.

Replication in Experiments

Each treatment can be tested multiple times in an experiment in order to increase the degrees of freedom and improve the capability of analysis. We call this method replication.
Replicates are the number of repetitions of running an individual treatment, which increase the power of the experimental responses. The order to run the treatments in an experiment should be randomized to minimize the noise.
Advantages of replication include: helps to better identify the true sources of variation, helps estimate the true impacts of the factors on the response, and overall improves the reliability and validity of the experimental results.

2² Full Factorial DOE

Case study: We are running a 2² full factorial DOE to discover the cause-and-effect relationship between the cake tastiness and two factors: temperature of the oven and time length of baking. Each factor has two levels and there are four treatments in total.
We decide to run each treatment twice so that we have enough degrees of freedom to measure the impact of two factors and the interaction between two factors. Therefore, there are eight observations in response eventually.

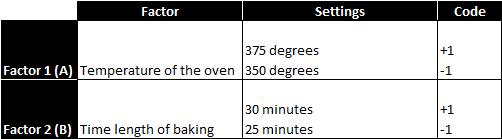
The objective is to understand the main effects and the interactions of these factors on the response variable. After running the four treatments twice in a random order, we obtain the following results

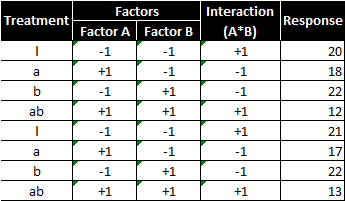
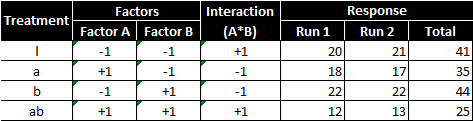
There are two factors and two levels, so there would be 2^2 = 4 treatment combinations. With replicates, each treatment combination is repeated once; therefore, there are in total 8 runs in this experiment. The experiment results are consolidated into the following table

The main effect of factor A is computed by averaging the difference between combinations where A was at its high settings and where A was at its low settings.
Main effect of factor A (temperature of the oven):

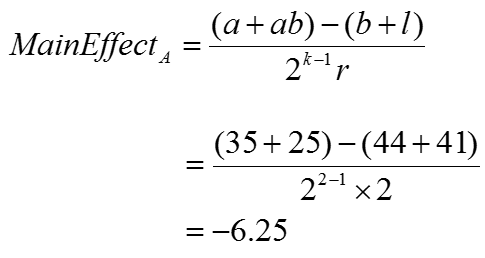
Where:

[unordered_list style=”star”]

• k is the number of factors
• r is the number of times individual treatments are being run

[/unordered_list]

Using the formula provided, the main effect of increasing the temperature of the oven is to decrease tastiness of the cake by −6.25.

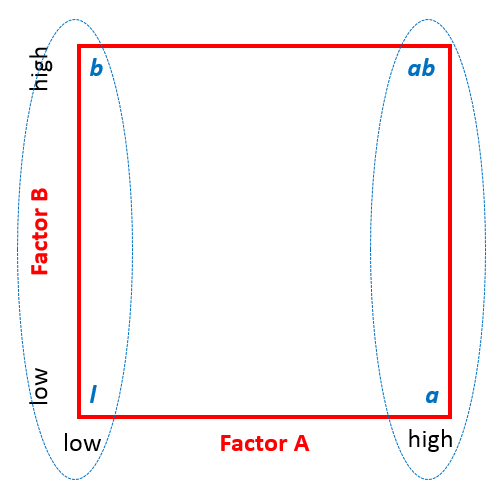
The main effect of factor B, similar to A, is computed by averaging the difference between combinations where B was at its high settings and where B was at its low settings.
Main effect of factor B (time length of baking):

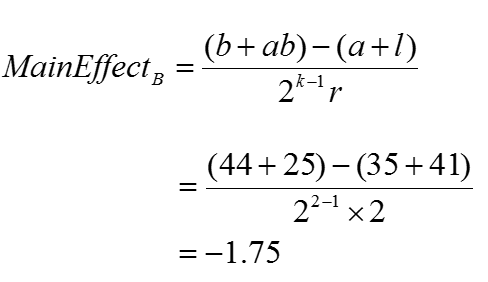
Where:

[unordered_list style=”star”]

• k is the number of factors
• r is the number of times individual treatments are being run

[/unordered_list]

Using the formula provided, the main effect of increasing the baking time is to decrease the tastiness of the cake by −1.75

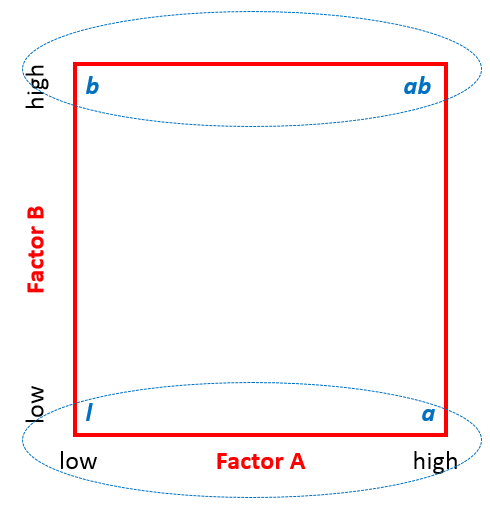
The interaction effect is computed by averaging the difference between combinations where A and B were at opposite settings (low and high).

Interaction (i.e. A*B) effect:

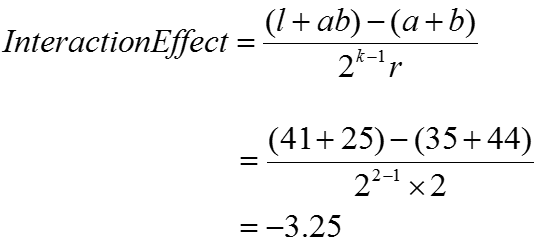
Where:

[unordered_list style=”star”]

• k is the number of factors
• r is the number of times individual treatments are being run

[/unordered_list]

Using the formula provided, the interaction effect of the temperature and time variables on tastiness was −3.25.

Sum of squares of factors and interaction

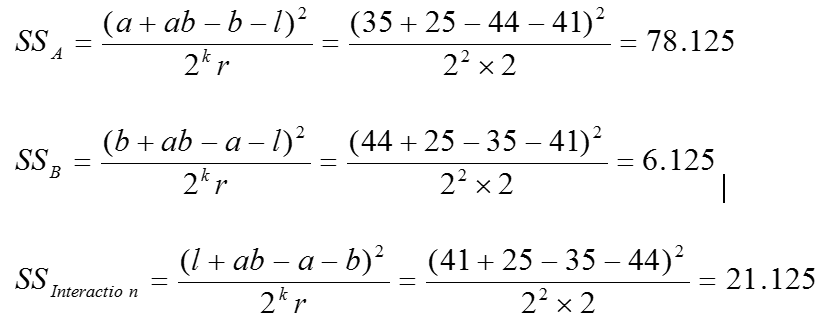
Where:

[unordered_list style=”star”]

• k is the number of factors
• r is the number of times individual treatments are being run

[/unordered_list]

The sum of squares tells us the relative strength of each main effect and interaction. A has the strongest effect as indicated by the high SS value. The degrees of freedom are necessary to determine the mean squares value.

Degrees of freedom of factors and interaction:

Four degrees of freedom are necessary because there are three effects we are looking to understand: factor A, factor B, and the interaction between them.

Mean squares of factors and interaction:

Use SigmaXL to Run a 2k Full Factorial DOE

Step 1: Initiate the experiment design

1. Click SigmaXL -> Design of Experiments -> 2-Level Factorial/Screening -> 2-Level Factorial/Screening Designs
2. A new window named “2-Level Factorial/Screening Design of Experiments” pops up
3. Select “1” as the Number of Responses.
4. Enter “Tastiness” into the “Response Name” box.
5. Select “2” as the Number of Factors
6. Select “4-Run, 2**2, Full-Factorial” as the design
7. Select “2” as the Number of Replicates
8. Enter “Temp” as the name for factor A
9. Enter “Time” as the name for factor B
   
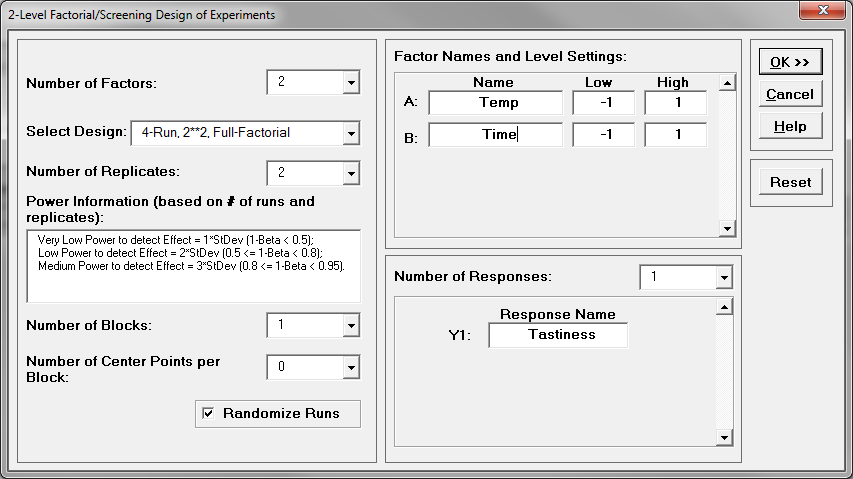
10. Click “OK>>”
11. The 2² full factorial DOE template appears in the newly generated tab “2 Factor DOE”.
    

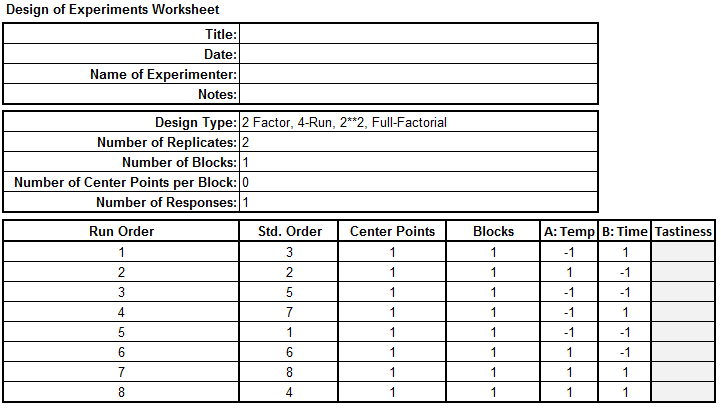
Step 2: Run the experiment and record the response in the table created by SigmaXL. The data has been provided for you in the DOE Full Factorial data table in your Sample Data.xlsx file. Carefully (paying close attention to using the “Temp” and “Time” settings to map your “Tastiness” results) enter the “Tastiness” values into your newly generated DOE template.

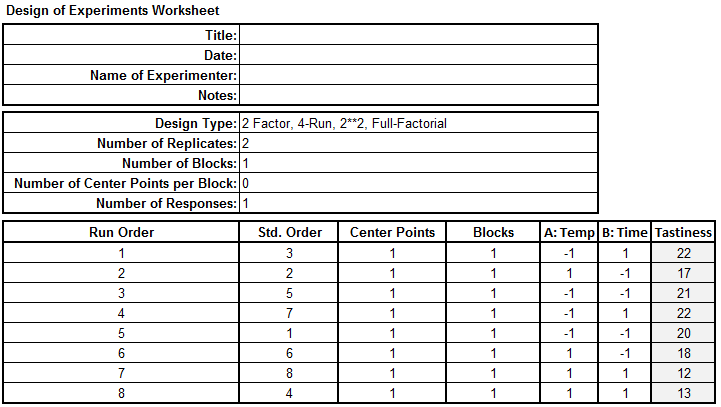Step 3: Analyze the experiment results

1. Click SigmaXL -> Design of Experiments -> 2-Level Factorial/Screening -> Analyze 2-Level Factorial/Screening Design
2. A new window named “Analyze 2-Level Factorial/Screening Design” appears in which “Tastiness” is automatically selected as the response variable and three factors including the interaction term are automatically selected as the independent variables.
   
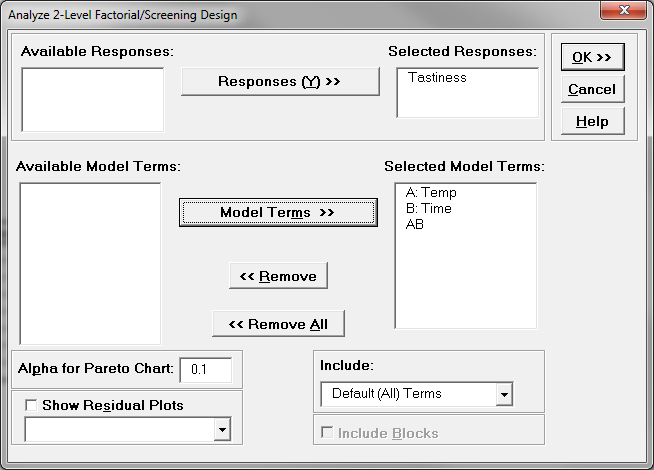
3. Click “OK”
4. The DOE analysis results appear in the newly generated tab “Analyze – 2 Factor DOE”.
   

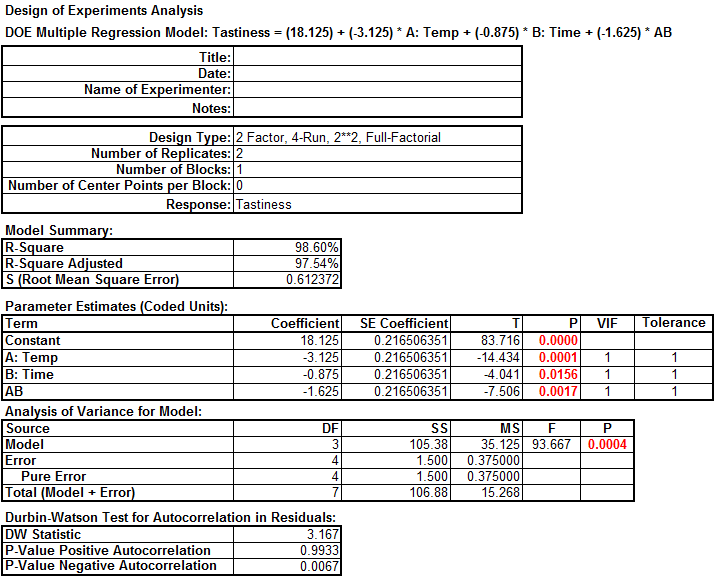
These are the results, Since the p-values of all the independent variables in the mode are smaller than the alpha level (0.05), both factors and their interaction have statistically significant impact on the response. High R² value shows around 98% of the variation in the response can be explained by the model (very good results).

Enter the actual settings of the independent variables into the yellow cells on the “Analyze – 2 Factor DOE” tab. The predicted response will be calculated automatically.

Model summary: These are the software outputs for expected/predicted results, as well as the residuals for each combination.